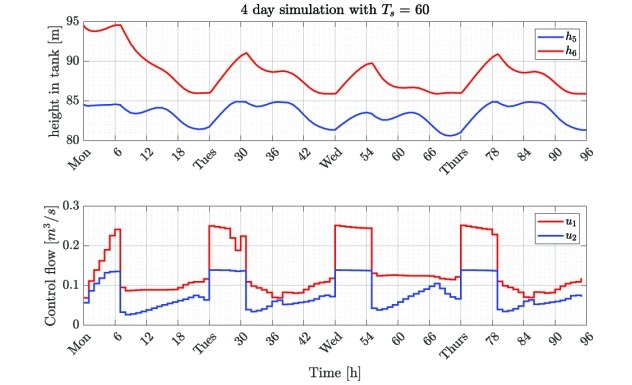
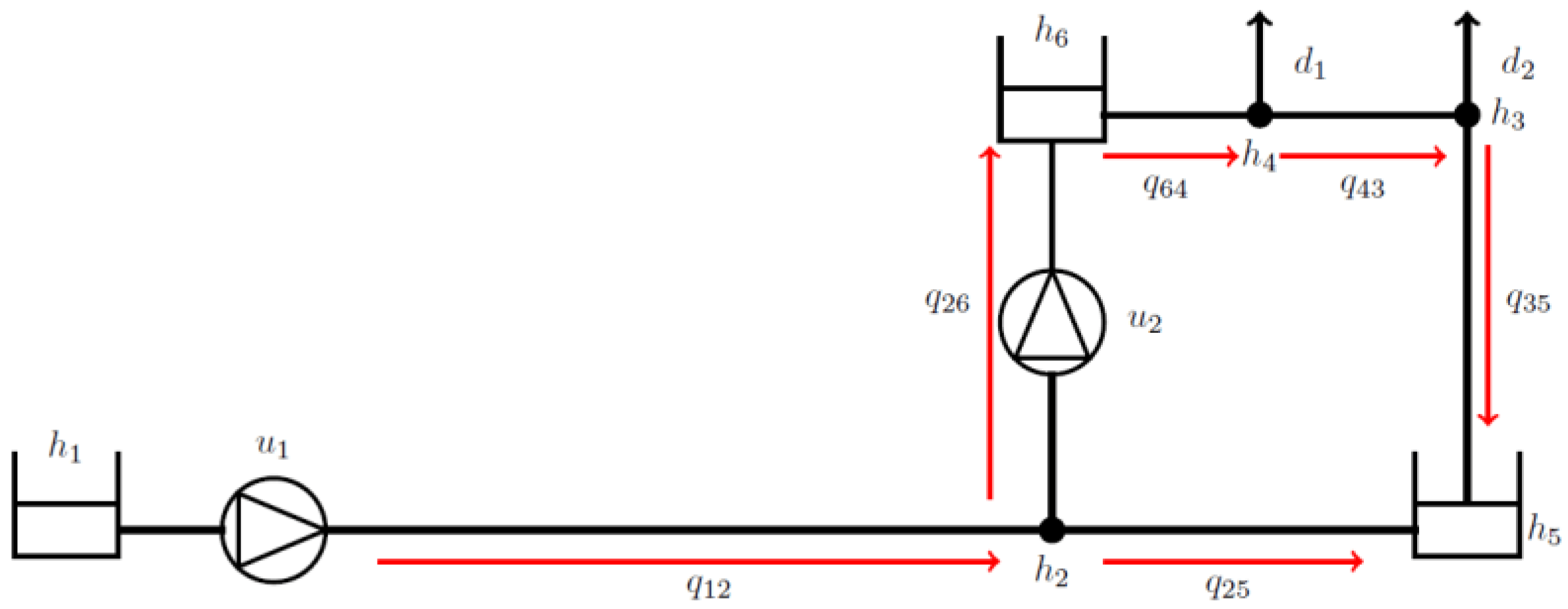
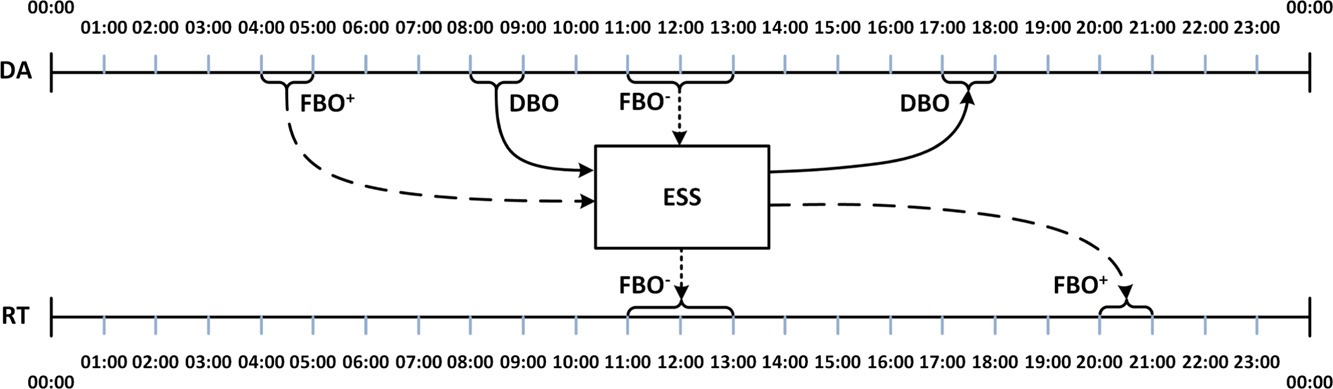
In this paper, we propose a parallel shooting algorithm for solving nonlinear model predictive control problems using sequential quadratic programming. This algorithm is built on a two-phase approach where we first test and assess sequential convergence over many initial trajectories in parallel. However, if none converge, the algorithm starts varying the Newton step size in parallel instead. Through this parallel shooting approach, it is expected that the number of iterations to converge to an optimal solution can be decreased. Furthermore, the algorithm can be further expanded and accelerated by implementing it on GPUs. We illustrate the effectiveness of the proposed Parallel Shooting Sequential Quadratic Programming (PS-SQP) method in some benchmark examples for nonlinear model predictive control. The developed PS-SQP parallel solver converges faster on average and especially when significant nonlinear behaviour is excited in the NMPC horizon. Read more here: https://ieeexplore.ieee.org/abstract/document/10252893